Формула, определяющая значение тока - его сущность, составляющие и методы расчета

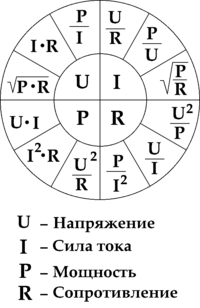
В физике существует ряд фундаментальных понятий, которые играют важную роль в понимании многих явлений и процессов. Одним из таких понятий является «ток». В нашей повседневной жизни мы сталкиваемся с ним постоянно, хотя не всегда осознаем это. Ток – это поток электрических зарядов, который проходит через проводник. Он является одним из основных параметров, определяющих работу электрических устройств и схем.

Для того чтобы выражать и учитывать ток в математическом виде, используются специальные формулы. Такие формулы позволяют более точно описывать физические процессы, связанные с электричеством. Благодаря этому, мы можем не только вычислять величину тока, но и анализировать его изменения в зависимости от различных факторов.

Одной из основных формул, связанных с током, является уравнение, определяющее его величину. Оно выражает зависимость между силой тока, напряжением и сопротивлением проводника. Именно с помощью этой формулы мы можем рассчитать показатели тока в конкретных ситуациях и прогнозировать его поведение при изменении внешних условий.

Определение тока: изучаем основы электрического потока

Основные характеристики тока

Направленность: ток может быть постоянным (в одном направлении) или переменным (с меняющимся направлением).
Сила тока: определяет количество заряда, протекающего через единицу времени и измеряется в амперах.
Напряжение: разница потенциалов между точками, вызывающая движение заряда через проводник.

Законы, описывающие ток

Движение тока подчиняется определенным законам. Один из основных законов — закон Ома, который устанавливает пропорциональность между напряжением, силой тока и сопротивлением проводника. Согласно этому закону, ток пропорционален напряжению и обратно пропорционален сопротивлению.

Также стоит упомянуть о законе Кирхгофа, который формулирует закон сохранения электрического заряда в узле и закон сохранения энергии в замкнутом контуре.

Более сложные формулы и уравнения могут использоваться для более точного описания свойств и поведения тока в различных ситуациях. Однако, для понимания основных принципов и приложений тока, знание указанных законов уже является существенным шагом вперед.

Определение и основные характеристики тока

Понятие электрического тока

Электрический ток – это движение носителей заряда, таких как электроны, внутри проводника при наличии разности потенциалов. По сути, это поток заряженных частиц, который возникает под влиянием электрического поля. Ток может быть постоянным или переменным в зависимости от типа электрической схемы.

Характеристики электрического тока

Основные характеристики тока – это его направление, величина и частота изменения. Направление тока определяется положительными и отрицательными зарядами, которые движутся в противоположных направлениях. Величина тока измеряется в амперах и характеризует количество зарядов, проходящих через поперечное сечение проводника за единицу времени. Частота изменения, или частота тока, определяет частоту колебаний заряда.

Основные характеристики электрического потока: мощность, направление, интенсивность

Характеристика	Описание
Мощность	Эта характеристика определяет количество энергии, передающейся через проводник в единицу времени. Мощность измеряется в ваттах и позволяет оценить эффективность потока электричества.
Направление	Направление электрического потока определяется положительными и отрицательными зарядами, которые движутся по проводникам. Важно знать направление потока для правильной организации электрической схемы и корректного подключения устройств.
Интенсивность	Интенсивность тока описывает силу движения зарядов в потоке. Она измеряется в амперах и позволяет определить силу тока в проводнике. Высокая интенсивность может быть опасной, поэтому важно соблюдать меры предосторожности при работе с электричеством.

Знание этих характеристик позволяет понимать основные принципы работы электрического потока и применять их в практических ситуациях. Например, при проектировании электрической сети или выборе правильного проводника для определенной нагрузки. Также они играют важную роль в диагностике и ремонте электронных устройств.

Закон Ома и вычисление электрического тока

Значение закона Ома

Закон Ома устанавливает связь между напряжением, силой тока и сопротивлением в электрической цепи. Согласно этому закону, сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению в цепи. Иными словами, чем больше напряжение и меньше сопротивление, тем больше ток протекает через цепь.

Формула, описывающая закон Ома, имеет вид: сила тока = напряжение / сопротивление. Это позволяет производить вычисления тока в электрической цепи, зная значения напряжения и сопротивления.

Вычисление тока в электрической цепи

Для вычисления тока в электрической цепи необходимо знать значения напряжения, которое подается на цепь, и сопротивление самой цепи. Напряжение может быть измерено с помощью вольтметра, а сопротивление может быть известно либо по значению резистора, либо может быть вычислено с использованием закона Ома и известных значений напряжения и тока.

Для вычисления тока в электрической цепи по формуле закона Ома, необходимо разделить значение напряжения на значение сопротивления. Полученное значение будет представлять собой силу тока, протекающего через эту цепь при указанном напряжении и сопротивлении.

Шаг 1: Измерить или знать напряжение, подаваемое на цепь;
Шаг 2: Измерить или определить сопротивление электрической цепи;
Шаг 3: Используя формулу закона Ома, разделить значение напряжения на значение сопротивления;
Шаг 4: Полученное значение будет являться силой тока в данной электрической цепи.

Вычисление тока в электрической цепи позволяет понять, какой объем электрического тока протекает через цепь при заданных условиях. Эта информация является важной для проектирования и использования электрических систем в различных областях, начиная от промышленности до домашнего использования.

Закон и его значения в электротехнике: основы и применения

Основной закон, который рассматривает ток, связан с двумя важными концепциями: напряжением и сопротивлением. Идея закона заключается в том, что ток течет через электрическую цепь только тогда, когда на нее действует электрическое напряжение, преодолевая сопротивление. Другими словами, существует прямая зависимость между напряжением и током в электрической цепи.

Значение этого закона заключается в возможности управления и распределения электрической энергии. Он позволяет определить, как будет вести себя электрический ток в различных системах и устройствах, что является основой для конструирования и эксплуатации электрических сетей, электронных устройств, моторов и трансформаторов.

Применение этого закона в электротехнике позволяет инженерам разрабатывать более эффективные электрические системы, учитывая энергосбережение, мощность и стабильность тока. Закон также является основой для более сложных математических моделей и уравнений, которые используются для анализа и проектирования электрических цепей и устройств в различных областях электротехники.

Соединение между напряжением и сопротивлением в электрической цепи

В электрической цепи возникает особое соотношение между напряжением и сопротивлением, которое позволяет рассчитать силу тока, протекающего через цепь. Это соединение описывается специальной формулой, которая позволяет нам понять, как изменение одной величины влияет на другую.

Взаимоотношение напряжения и сопротивления

При рассмотрении электрической цепи необходимо учесть взаимодействие двух основных элементов: напряжения и сопротивления. Напряжение в цепи вызывает поток электрического тока, а сопротивление препятствует этому потоку и определяет его интенсивность. Соотношение между этими двумя величинами позволяет рассчитать, какая сила тока будет протекать через цепь.

Закон Ома и формула для вычисления силы тока

Один из основополагающих законов в электрических цепях — закон Ома. Согласно этому закону, сила тока, протекающего по цепи, прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Именно эта взаимосвязь между силой тока, напряжением и сопротивлением описывается специальной формулой, которая позволяет рассчитать силу тока при известных значениях напряжения и сопротивления в цепи.

Практические примеры использования формулы для расчета

Этот раздел представляет собой набор практических примеров, в которых иллюстрируются возможности и применение формулы для расчета. В этих примерах мы рассмотрим различные сферы, в которых формула может быть полезна, а также покажем, как она может помочь в решении реальных задач.

Пример 1: Расчет скорости движения автомобиля

Одной из самых распространенных ситуаций, где формула может быть полезной, является определение скорости движения автомобиля. В данном примере мы рассмотрим, как с использованием формулы можно точно определить скорость автомобиля исходя из данных о пройденном расстоянии и затраченном времени.

Пример 2: Расчет процентного соотношения

Другой важный пример применения формулы для расчета — определение процентного соотношения. В данном примере мы рассмотрим, как формула может быть использована для вычисления процентного соотношения в различных ситуациях, таких как определение доли продаж конкретного товара от общего объема продаж.

Таким образом, формула для расчета может быть полезным инструментом в различных задачах, связанных с вычислениями и определением соотношений. Практические примеры, представленные в этом разделе, помогут вам лучше понять, как использовать эту формулу в реальных ситуациях и получить точные и достоверные результаты.

Расчет электрических цепей с известными значениями напряжения и сопротивления

В данном разделе мы рассмотрим методы расчета простых электрических цепей, где известны значения напряжения и сопротивления. Эти расчеты помогут нам определить значение тока, текущего через цепь, используя доступные нам формулы и законы электричества.

Закон Ома

Один из основных законов, используемых при расчете электрических цепей, — это закон Ома. Согласно этому закону, ток через цепь прямо пропорционален напряжению и обратно пропорционален сопротивлению:

Ток = Напряжение / Сопротивление

Пример расчета

Давайте рассмотрим пример простой электрической цепи, состоящей из одного резистора, с известными значениями напряжения и сопротивления. Пусть напряжение на цепи равно 12 В, а сопротивление резистора составляет 4 Ом.

Используя закон Ома, мы можем легко рассчитать значение тока через цепь:

Напряжение: 12 В
Сопротивление: 4 Ом

Ток = 12 В / 4 Ом = 3 А

Таким образом, в данном примере ток, текущий через цепь, составляет 3 Ампера.

Расчеты простых электрических цепей с известными значениями напряжения и сопротивления важны для понимания и проектирования различных электрических систем. Они позволяют определить, какие значения тока будут протекать через цепь при заданных условиях и помогают в дальнейшем рассчитывать электрическую мощность, энергию и другие характеристики системы. Используя соответствующие формулы и законы, можно с уверенностью прогнозировать и контролировать работу электрических цепей для оптимального функционирования устройств.