Расчет формулы ампер – основа эффективного использования электрического тока и мощных устройств

Все вокруг нас переполнено электричеством, и для эффективного функционирования многочисленных электрических устройств необходимо внимательно изучать и понимать законы и принципы, определяющие их работу. Одной из важнейших физических величин в области электричества является мощность электрического тока. Знание этого показателя позволяет не только оценить эффективность работы устройств, но и правильно применять их в различных ситуациях.

Мощность электрического тока, представляющая собой работу, совершенную током в единицу времени, является одной из фундаментальных характеристик электрической системы. Устанавливать мощность удобно с помощью специальной формулы, которая позволяет получить точное значение данной величины. При расчете мощности учитываются не только сила тока, но и другие факторы, влияющие на эффективность работы устройства.

Применение формулы расчета мощности электрического тока позволяет более глубоко понять процессы, происходящие в системе электрического тока. Использование данного инструмента делает возможным не только оценку эффективности и экономичности работы устройства, но и позволяет осуществлять предварительный анализ и планирование электроэнергетических процессов. Учитывая постоянное развитие технологий и увеличение числа электрических устройств, понимание и применение формулы расчета мощности электрического тока становится все более актуальным для обеспечения безопасной и стабильной работы подключенных устройств.

Основные понятия и принципы расчета тока в электрических цепях

При анализе электрической цепи важно учесть два основных понятия: напряжение и сопротивление. Напряжение, или электрический потенциал, указывает на разность потенциалов между двумя точками в цепи. Сопротивление, в свою очередь, описывает трудность с протеканием электрического тока через материал или устройство.

• Напряжение можно представить как «силу», с которой электроны движутся по цепи.
• Сопротивление можно сравнить с «преградами», наличие которых затрудняет движение электронов.

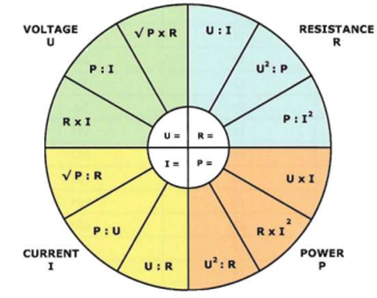
Важно понимать, что сила тока, т.е. количество электронов, протекающих через участок цепи в единицу времени, зависит от величины напряжения и сопротивления по формуле, наиболее полно и точно описывающей эту зависимость: сила тока = напряжение / сопротивление.

Для наглядности и понимания данной формулы, можно представить условный пример с водой: если мы практически зажимаем шланг (увеличиваем сопротивление), при одинаковом давлении в системе (напряжении), количество воды, протекающей через шланг, снижается.

Закон Ома и его практическое применение

Раздел «Закон Ома и его практическое применение» представляет обширные возможности для достижения электрического равновесия и определения силы электрического тока в цепи с помощью фундаментального принципа взаимодействия в электрической системе. Этот принцип, названный в честь Ома за его открытие, позволяет анализировать и управлять токами и напряжениями.

Описание Закона Ома обращает внимание на зависимость между напряжением в цепи, силой электрического тока и электрическим сопротивлением. По сути, закон Ома может быть представлен как равенство, связывающее разницу потенциалов силой тока и сопротивлением. Более простыми словами, этот закон позволяет определить, как сила тока влияет на работу электрической цепи в зависимости от ее сопротивления.

Понимание Закона Ома является ключевым элементом в различных областях науки и техники, таких как электрические сети, электроника, электротехника и многие другие. Соответствующая экспертиза в области применения Закона Ома может помочь в создании эффективных электрических систем, от простых устройств до сложных сетей. Понимание взаимодействия между током, напряжением и сопротивлением позволяет разрабатывать электрические цепи, которые обеспечивают необходимую функциональность и безопасность.

Важно отметить, что понимание и применение Закона Ома требуют точности и аккуратности при расчетах и проектировании электрических систем.

Использование Закона Ома позволяет ученным, инженерам и электрикам определить параметры электрических цепей, такие как сопротивление, сила тока, напряжение и мощность, что позволяет разработать оптимальные решения для широкого спектра приложений.

Важность сопротивления в электрической цепи

Сопротивление может проявляться в разных объектах и компонентах электрической цепи, включая проводники, резисторы, диоды и другие устройства. Каждый материал имеет свой уникальный уровень сопротивления, который зависит от его физических и химических свойств. Некоторые материалы обладают высоким сопротивлением, таким образом затрудняя прохождение тока, в то время как другие материалы обладают низким или даже нулевым сопротивлением, что способствует плавному движению тока.

Сопротивление также влияет на энергию, которая трансформируется и теряется в процессе прохождения тока через электрическую цепь. Большое сопротивление может привести к большим потерям энергии в виде тепла, что может оказаться нежелательным в некоторых системах. Отношение сопротивления к энергии тока в цепи определяет его эффективность и потенциал для использования в различных приложениях.

Важные аспекты сопротивления:
Сдерживание тока
Уникальность материалов
Влияние на энергию
Эффективность и применимость

Применение закона Ома для расчета силы электрического тока

В электротехнике существует закон, который описывает взаимосвязь между напряжением, силой тока и сопротивлением в электрической цепи. Этот закон, названный в честь Георга Симона Ома, позволяет определить силу тока по известным значениям напряжения и сопротивления.

Применение закона Ома для расчета силы тока основано на простой формуле, которая устанавливает, что сила тока пропорциональна напряжению и обратно пропорциональна сопротивлению в цепи. Таким образом, при известных значениях напряжения и сопротивления возможно вычислить силу тока, протекающего в цепи.

Для применения закона Ома к расчету силы тока необходимо знать величину напряжения, измеряемую в вольтах, и сопротивление, измеряемое в омах. Закон Ома формализует эту взаимосвязь и позволяет с уверенностью рассчитать силу тока, что является важным аспектом в множестве электрических схем и устройств.

• Используя известные значения напряжения и сопротивления, можно определить силу тока с помощью формулы, полученной из закона Ома.
• Полученные значения силы тока могут быть использованы для определения эффективного функционирования электрических цепей и устройств.
• Расчет силы тока позволяет электрикам и инженерам принимать решения о необходимости изменения значений напряжения или сопротивления для достижения оптимальной работы системы.

В итоге, применение закона Ома для расчета силы тока является важным инструментом для электротехников, позволяющим анализировать и проектировать электрические цепи, а также обеспечивать эффективную работу электрооборудования. Знание этого закона и его применения помогает в области электрики и электроники, позволяя эффективно управлять электрическими системами и устройствами.

Применение и практические примеры использования расчетной формулы для определения силы тока

В данном разделе мы рассмотрим различные ситуации, где необходимо проводить расчеты силы тока в электрической цепи. Определение собственной силы тока способно помочь в решении различных проблем, связанных с электротехникой. Знание принципа расчетной формулы позволяет эффективно управлять электрическими системами, а также решать практические задачи.

Представим себе ситуацию, когда необходимо определить силу тока внутри электрической цепи, но она не предназначена для простого измерения. В таких случаях нам на помощь придет расчетная формула, которая использует различные параметры цепи. Например, мы можем применить эту формулу для определения силы тока, протекающего через определенный сопротивитель в цепи, или для определения суммарной силы тока при использовании нескольких параллельных сопротивлений.

В таблице ниже приведены примеры и практические задачи, в которых применяется расчетная формула для определения силы тока. Каждый пример содержит основные параметры цепи и шаги, необходимые для расчета. Эти примеры помогут вам лучше понять, как использовать расчетную формулу на практике и применять ее для решения конкретных задач.

Пример	Параметры цепи	Шаги расчета
Пример 1	Сопротивление, напряжение	Расчет по формуле
Пример 2	Сопротивления в параллель, напряжение	Расчет по формуле
Пример 3	Сопротивление, сопротивления в серии, напряжение	Расчет по формуле

В нашем примере мы использовали несколько ситуаций, чтобы продемонстрировать разнообразие практического использования расчетной формулы для определения силы тока. Конечно, существует множество других ситуаций, где также может быть полезно использование данной формулы. Знание и понимание этого инструмента позволяет успешно решать различные электротехнические задачи и обеспечивать эффективную работу электрических систем.

Сила тока в простых электрических цепях: разбор основных понятий

В ходе расчета силы тока в простых электрических цепях мы изучим основные понятия, связанные с этим явлением. Мы рассмотрим, как заряды перемещаются по проводникам, на всем их протяжении, и как это влияет на общую силу тока в цепи. Анализируя связь между напряжением, сопротивлением и силой тока, мы сможем лучше понять, как работают основные элементы простых электрических цепей и как влияют на эффективность и функциональность системы.

Для полного понимания силы тока необходимо изучить и разобрать формулы, связанные с данным явлением. В результате этого анализа, мы сможем легко выполнять расчеты и прогнозировать электрические параметры в простых электрических цепях. В данном разделе мы не будем обсуждать конкретные расчеты, но сфокусируемся на понимании основных принципов и формул, чтобы в будущем легко применять их в практических задачах.

Расчет силы тока в сложных электрических цепях при наличии различных элементов

В данном разделе мы рассмотрим методы расчета силы тока в электрических цепях, состоящих из различных элементов. При расчете учитываются сопротивление проводов, резисторы, конденсаторы и другие компоненты, которые могут встречаться в сложных электрических цепях.

Для точного расчета силы тока в таких цепях необходимо использовать законы Кирхгофа. Закон Кирхгофа о силе тока гласит, что алгебраическая сумма токов, втекающих и вытекающих из любой узловой точки в цепи, равна нулю. Используя этот закон, можно определить силу тока в каждом элементе цепи и произвести расчет, учитывая взаимодействие всех элементов.

Одним из методов расчета силы тока в сложных электрических цепях является применение метода эквивалентного сопротивления. Суть метода заключается в замене всей сети проводов, резисторов и других элементов цепи одним эквивалентным резистором, который имеет те же самые электрические свойства, что и исходная цепь. После замены цепь считается простой и силу тока можно рассчитать по обычным формулам.

• Для расчета силы тока в цепях с использованием метода эквивалентного сопротивления необходимо:
1. Определить все элементы цепи и их электрические характеристики.
2. Составить схему цепи и обозначить все известные величины.
3. Применить закон Кирхгофа для определения силы тока в узлах цепи.
4. Заменить всю сеть элементов одним эквивалентным сопротивлением.
5. Рассчитать силу тока по формуле, используя уже полученное эквивалентное сопротивление.

Таким образом, расчет силы тока в сложных электрических цепях требует применения методов анализа цепей и использования законов Кирхгофа. Метод эквивалентного сопротивления позволяет упростить расчеты и получить точные значения силы тока в любой точке цепи.

Ограничения в применении формулы ампер: важные аспекты, которые необходимо учитывать

При изучении электромагнетизма и проведении расчетов связанных с ним, необходимо учитывать ряд ограничений и особых условий применения формулы ампер, которые помогут правильно интерпретировать полученные результаты и избежать ошибок.

• Среда распространения: формула ампер предназначена для применения в свободном пространстве, однако не всегда возможно полностью исключить влияние окружающей среды. Например, в случае использования проводников и других материалов с непостоянными характеристиками, необходимо учесть их влияние на расчеты.
• Ограничения в геометрии: применение формулы ампер осуществляется для простых геометрических конфигураций, включающих однородные проводники или соленоиды. При расчетах более сложных систем, таких как круговые петли или системы с изменяющимся поперечным сечением, возникают дополнительные условия и ограничения.
• Влияние переменного тока: формула ампер является результатом закона ома, который работает только для постоянного тока. В случае переменного тока возникают дополнительные сложности и необходимость использования других методов расчета.
• Релевантность масштаба: формула ампер применима при определенных масштабах задачи. Если размеры и характеристики взаимодействующих объектов существенно отличаются от расчетов по формуле ампер, необходимо использовать альтернативные методы расчета.

Учитывая эти важные аспекты, и уделяя достаточное внимание ограничениям применения формулы ампер, можно добиться более точных и надежных результатов в расчетах и анализе электрических и магнитных явлений.

Влияние температуры на электрическое сопротивление: важный фактор для расчета электрического тока

Сопротивление — это свойство материала сопротивляться потоку электрического тока. Изменение сопротивления вещества происходит под влиянием изменения температуры. Расчет и понимание этой взаимосвязи являются важными для различных областей науки и техники.

Когда температура вещества повышается, его сопротивление возрастает. Такое изменение объясняется изменениями в количестве свободных электронов и других носителей заряда, а также в движении электронов внутри материала. Это влияние температуры возможно измерить и описать с помощью математических формул и дополнительных физических параметров.

Факторами, влияющими на изменение сопротивления вещества при изменении температуры, являются:

• Коэффициент температурного расширения материала
• Уровень энергии, связанный с движением электронов и носителей заряда
• Свойства электронов, такие как подвижность и столкновения с атомами

Зная эти параметры и проведя соответствующие расчеты, можно оценить изменение сопротивления проводников при изменении температуры. Это рассчитанное значение сопротивления является важным параметром при расчете электрического тока. Учет влияния температуры на сопротивление позволяет обеспечить правильность и точность расчетов, а также улучшить производительность и эффективность электрических систем.

Видео: