Закон Кулона простым языком

Электрические заряды и электрификация тел

Электрические заряды, положительные и отрицательные, квантуются, то есть имеют наименьшее значение, которое дальше невозможно разделить. Нагрузки не могут быть созданы или уничтожены в том смысле, что общая нагрузка в любом процессе остается постоянной. Когда атом не ионизирован, его полный заряд равен нулю. Атомы с избыточным отрицательным зарядом называются анионами, а с недостатком отрицательного заряда (с избыточным положительным зарядом) мы называем катионами.

Электрификация тел заключается в переносе нагрузки с одного из них на другой. Проще говоря, тела могут быть наэлектризованы их взаимным трением, что связано с реконструкцией двойного электрического слоя, расположенного на поверхности каждого из этих тел. Другим способом электрификации является электрификация индукцией, как показано на рисунках ниже. Здесь металлические сферы (белые), установленные на изоляторе (черный стержень), подвергаются электрификации. Разделение зарядов происходит при приближении к отрицательно заряженному изоляционному стержню, наэлектризованному трением о ткань.

В системе СИ единица измерения составляет 1 кулон (1 С). Статический заряд составляет порядка 10 -6 С (микрокульм, около 10 13 электронов). Заряд электрона составляет 1,602 × 10 -19 с .

История открытия

Эксперименты с заряженными частицами проводили много физиков:

• Г. В. Рихман;
• профессор физики Ф. Эпинус;
• Д. Бернулли;
• Пристли;
• Джон Робисон и многие другие.

Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.

Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).

Рис. 2. Крутильные весы

У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10-9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1º. Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.

Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.

Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.

Это интересно: Как лудить провода – простой способ лужения

Отрывок, характеризующий Кулон

– Мне сделали пропозицию насчет вас, – сказал он, неестественно улыбаясь. – Вы, я думаю, догадались, – продолжал он, – что князь Василий приехал сюда и привез с собой своего воспитанника (почему то князь Николай Андреич называл Анатоля воспитанником) не для моих прекрасных глаз. Мне вчера сделали пропозицию насчет вас. А так как вы знаете мои правила, я отнесся к вам. – Как мне вас понимать, mon pere? – проговорила княжна, бледнея и краснея. – Как понимать! – сердито крикнул отец. – Князь Василий находит тебя по своему вкусу для невестки и делает тебе пропозицию за своего воспитанника. Вот как понимать. Как понимать?!… А я у тебя спрашиваю. – Я не знаю, как вы, mon pere, – шопотом проговорила княжна. – Я? я? что ж я то? меня то оставьте в стороне. Не я пойду замуж. Что вы? вот это желательно знать. Княжна видела, что отец недоброжелательно смотрел на это дело, но ей в ту же минуту пришла мысль, что теперь или никогда решится судьба ее жизни. Она опустила глаза, чтобы не видеть взгляда, под влиянием которого она чувствовала, что не могла думать, а могла по привычке только повиноваться, и сказала: – Я желаю только одного – исполнить вашу волю, – сказала она, – но ежели бы мое желание нужно было выразить… Она не успела договорить. Князь перебил ее. – И прекрасно, – закричал он. – Он тебя возьмет с приданным, да кстати захватит m lle Bourienne. Та будет женой, а ты… Князь остановился. Он заметил впечатление, произведенное этими словами на дочь. Она опустила голову и собиралась плакать. – Ну, ну, шучу, шучу, – сказал он. – Помни одно, княжна: я держусь тех правил, что девица имеет полное право выбирать. И даю тебе свободу. Помни одно: от твоего решения зависит счастье жизни твоей. Обо мне нечего говорить. – Да я не знаю… mon pere. – Нечего говорить! Ему велят, он не только на тебе, на ком хочешь женится; а ты свободна выбирать… Поди к себе, обдумай и через час приди ко мне и при нем скажи: да или нет. Я знаю, ты станешь молиться. Ну, пожалуй, молись. Только лучше подумай. Ступай. Да или нет, да или нет, да или нет! – кричал он еще в то время, как княжна, как в тумане, шатаясь, уже вышла из кабинета. Судьба ее решилась и решилась счастливо. Но что отец сказал о m lle Bourienne, – этот намек был ужасен. Неправда, положим, но всё таки это было ужасно, она не могла не думать об этом. Она шла прямо перед собой через зимний сад, ничего не видя и не слыша, как вдруг знакомый шопот m lle Bourienne разбудил ее. Она подняла глаза и в двух шагах от себя увидала Анатоля, который обнимал француженку и что то шептал ей. Анатоль с страшным выражением на красивом лице оглянулся на княжну Марью и не выпустил в первую секунду талию m lle Bourienne, которая не видала ее. «Кто тут? Зачем? Подождите!» как будто говорило лицо Анатоля. Княжна Марья молча глядела на них. Она не могла понять этого. Наконец, m lle Bourienne вскрикнула и убежала, а Анатоль с веселой улыбкой поклонился княжне Марье, как будто приглашая ее посмеяться над этим странным случаем, и, пожав плечами, прошел в дверь, ведшую на его половину. Через час Тихон пришел звать княжну Марью. Он звал ее к князю и прибавил, что и князь Василий Сергеич там. Княжна, в то время как пришел Тихон, сидела на диване в своей комнате и держала в своих объятиях плачущую m lla Bourienne. Княжна Марья тихо гладила ее по голове. Прекрасные глаза княжны, со всем своим прежним спокойствием и лучистостью, смотрели с нежной любовью и сожалением на хорошенькое личико m lle Bourienne.

Потенциал электростатического поля. Разность потенциалов

Как известно, если на тело действует какая-либо сила, то такое тело совершает определённую работу. Следовательно, и заряд, помещённый в электрическое поле, также будет выполнять работу. В электрическом поле выполненная зарядом работа не зависит от траектории движения, а определяется лишь положением, которое занимает частица в начале и конце перемещения. В физике поля подобные электрическому полю (где работа не зависит от траектории движения тела) называются потенциальными.

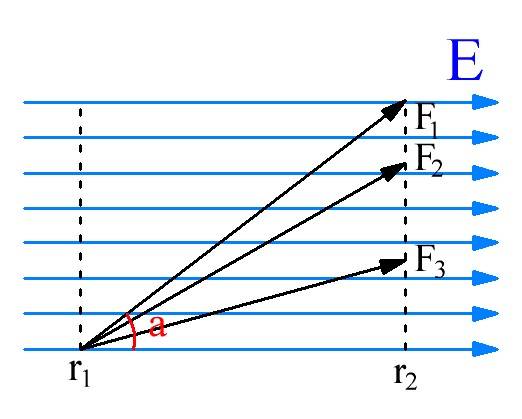
Выполненная телом работа определяется по следующему выражению

где F – сила, действующая не тело,

S – расстояние, пройденное телом по действие силы F,

α – угол между направлением движения тела и направлением действия силы F.

Тогда работа выполненная «пробным зарядом» в электрическом поле созданным зарядом q 0 определится из закона Кулона

где q П – «пробный заряд»,

q 0 – заряд создающий электрическое поле,

r 1 и r 2 – соответственно расстояние между q П и q 0 в начальном и конечном положении «пробного заряда».

Так как выполнение работы связано с изменением потенциальной энергии W P , тогда

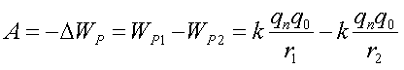
И потенциальная энергия «пробного заряда» в каждой отельной точке траектории движения будет определяться из следующего выражения

Как видно из выражения с изменением величины «пробного заряда» q п значение потенциальной энергии W P будет изменяться пропорционально q п, поэтому для характеристики электрического поля была введена ещё один параметр названный потенциалом электрического поля φ, который является энергетической характеристикой и определяется следующим выражением

где k – коэффициент пропорциональности, равный k = 1/(4πε 0) = 9 * 10 9 Кл 2 /(Н*м 2), где ε 0 – электрическая постоянная, ε 0 = 8,85 * 10 -12 Кл 2 /(Н*м 2).

Таким образом, потенциалом электростатического поля является энергетической характеристикой, которая характеризует потенциальную энергию, которой обладает заряд, помещённый в данную точку электростатического поля.

Из вышесказанного можно сделать вывод, что работа совершённая при перемещении заряда из одной точки в другую может быть определена из следующего выражения

То есть работа, совершаемая силами электростатического поля при перемещении заряда из одной точки в другую, равна произведению заряда на разность потенциалов в начальной и конечной точках траектории.

При расчётах наиболее удобно знать разность потенциалов между точками электрического поля, а не конкретные значения потенциалов в данных точках, поэтому говоря о потенциале какой либо точки поля, подразумевают разность потенциалов между данной точкой поля и другой точкой поля, потенциал которой условились считать равным нулю.

Разность потенциалов определяется из следующего выражения и имеет размерность Вольт (В)

Продолжение читайте в следующей статье

Теория это хорошо, но без практического применения это просто слова.

Определение 1

Электростатика – обширный раздел электродинамики, исследующий и описывающий покоящиеся в определенной системе электрически заряженные тела.

На практике выделяют два вида электростатических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть). Элементарный заряд является минимальным зарядом ($e = 1,6 ∙10^{ -19}$ Кл). Заряд любого физического тела кратен целому количеству элементарных зарядов: $q = Ne$.

Электризация материальных тел – перераспределение заряда между телами. Способы электризации: касание, трение и влияние.

Закон сохранения электрического положительного заряда – в замкнутой концепции алгебраическая сумма зарядов всех элементарных частиц остается стабильной и неизменной. $q_1 + q _2 + q _3 + …..+ q_n = const$. Пробный заряд в данном случае представляет собой точечный положительный заряд.

Применение закона Кулона на практике

Закон Кулона работает во всех областях современной электротехники. Данное утверждение справедливо, начиная с электрического тока, заканчивая простейшим заряженным конденсатором. Простейший случай — введение диэлектрика. Сила, с которой заряды взаимодействуют в вакууме, больше, чем сила взаимодействия аналогичных зарядов, разделенных диэлектрическим материалом.

Диэлектрической проницаемостью среды называют величину для количественного определения сил, независимо от расстояния между зарядами и от их величин. Чтобы рассчитать силу, которая будет действовать в присутствии диэлектрика, необходимо силу взаимодействия зарядов в вакууме поделить на диэлектрическую проницаемость внесенного диэлектрика.

С помощью изучения закона Кулона удается спроектировать сложное исследовательское оборудование в виде ускорителя заряженных частиц. Подобные установки функционируют на механизме взаимодействия электрического поля и заряженных частиц. Энергия частицы увеличивается за счет работы, которую совершает электрическое поле в ускорителе. Закон Кулона в этом случае полностью соблюдается, так как ускоряемую частицу можно рассмотреть в качестве точечного заряда, а действие ускоряющего электрического поля ускорителя представить в виде суммарной силы со стороны других точечных зарядов.

Направление частицы, исходя из силы Лоренца, определяет магнитное поле. Данная сила не воздействует на энергию и траекторию движения частиц в ускорителе.

К наиболее распространенным защитным электротехническим сооружениям относят молниеотводы. Работа данного устройства основана на законе Кулона. Гроза сопровождается появлением на Земле больших индуцированных зарядов. Заряды притягиваются в направлении грозовой тучи. В результате на поверхности планеты образуется мощное электрическое поле. В области острых проводников напряженность поля достигает больших значений. На заостренном наконечнике молниеприемника включается коронный заряд, который притягивается к заряду грозового облака, согласно закону Кулона. Около молниеотвода коронный заряд сильно ионизирует воздух, что приводит к уменьшению напряженности электрического поля вблизи острия. Индуцированные заряды не скапливаются на здании, что снижает вероятность возникновения молний. При ударе молнии заряд полностью будет отведен в землю без повреждения установки.

Примеры решения задач на напряженность электрического поля

Задача 1

В вакуумной среде расположена пара одинаковых положительных точечных зарядов. Расстояние между ними составляет r. Необходимо определить напряженность электрического поля в точке, которая равноудалена на расстояние r от этих зарядов.

Решение:

Исходя из принципа суперпозиции полей, напряженность, которую нужно вычислить, определяется геометрической суммой напряженностей полей, которые создаются зарядами. Формула будет иметь следующий вид:

\(\vec{E}=\vec{E_{1}}+\vec{E_{2}}\)

Модули напряженности полей зарядов определяются таким образом:

\(\vec{E_{1}}=\vec{E_{2}}=k\frac{q}{r^{2}}\)

Если с помощью векторов первого и второго электрических полей построить параллелограмм, то его диагональ будет обозначать напряженность результирующего поля. Модуль напряженности результирующего поля равен:

\(E=2E_{1}\cos 30^{0}=2k\frac{q}{r^{2}}\frac{\sqrt{3}}{2}=k\frac{q\sqrt{3}}{r^{2}}\)

Задача 2

Проводящая сфера, радиус (R) которой равен 0,2 метра, обладает зарядом (q) \(1,8*10^{-4}\) Кл. Сфера находится в вакуумной среде. Необходимо определить:

• модуль напряженности электрического поля \(\vec{E}\) на ее поверхности;
• модуль напряженности электрического поля \(\vec{E_{1}}\) в точке, которая удалена на расстояние \(r_1\) = 10 метров от центра сферы;
• модуль напряженности \(\vec{E_{0}}\) в центральной точке сферы.

Решение:

Электрическое поле, характерное для заряженной сферы, будет равно полю точечного заряда. Отсюда следует равенство:

\(E=k\frac{q}{r^{2}}\)

Таким образом, искомые величины можно рассчитать:

• \(E=k\frac{q}{R^{2}}=4\times 10^{7}\) (Н/Кл);
• \(E=k\frac{q}{r_{1}^{2}}=16\times 10^{3}\) (Н/Кл);
• напряженность поля в сфере, независимо от местонахождения точки, соответствует нулевому значению, то есть Е0 = 0.

Примечания

1. Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 67. — 240 с. — ISBN 5-7050-0118-5.

2. Производные единицы	Беккерель · Ватт · Вебер · Вольт · Генри · Герц · Градус Цельсия · Грей · Джоуль · Зиверт · Катал · Кулон · Люкс · Люмен · Ньютон · Ньютон-метр · · Паскаль · Радиан · Сименс · Стерадиан · Тесла · Фарад
   Принятые для использования с СИ	Ангстрем · Астрономическая единица · Гектар · Градус дуги (Минута дуги, Секунда дуги) · Дальтон (Атомная единица массы) · Децибел · Литр · Непер · Сутки (Час, Минута) · Тонна · Электронвольт Атомная система единиц · Естественная система единиц
   См. также	Приставки СИ · Система физических величин · Преобразование единиц · Новые определения СИ · История метрической системы
   Книга:СИ · Категория:СИ

   Это заготовка статьи о единицах измерения. Вы можете помочь проекту, дополнив её.

Как направлены силы

Заряды взаимодействуют друг с другом в зависимости от их полярности – одинаковые отталкиваются, а разноименные (противоположные) притягиваются.

Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r12 и как радиус-вектор от первого ко второму заряду и наоборот. Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:

Сила, приложенная к первому заряду со стороны второго обозначается как F12. Тогда в векторной форме закон Кулона выглядит следующим образом:

Для определения силы приложенной ко второму заряду используются обозначения F21 и R21.

Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.

Опыт Кулона

Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в. накопилось много качественных данных об электрических явлениях. Возникла потребность дать им количественную интерпретацию. Поскольку силы электрического взаимодействия были относительно невелики, возникла серьезная проблема в создании метода, который позволил бы произвести замеры и получить необходимый количественный материал.

Французский инженер и ученый Шарль Кулон предложил метод измерения малых сил, который основывался на следующем экспериментальном факте, обнаруженном самим ученым: сила, возникающая при упругой деформации металлической проволоки, прямо пропорциональна углу закручивания, четвертой степени диаметра проволоки и обратно пропорциональна ее длине:

где d – диаметр, l – длина проволоки, φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональности k находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.

Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10-8 Н.

Рис. 3

Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9 длиной 10,83 см, подвешенного на серебряной проволоке 5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик 8, а на другом – противовес 6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора 1. Здесь же имелся указатель 2, с помощью которого отсчитывался угол закручивания нити по круговой шкале 3. Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11. В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.

Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7 заряжался от предварительно наэлектризованного шарика 12. При соприкосновении шарика 7 с подвижным шариком 8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках 7 и 8.

Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9 поворачивалось на некоторый угол γ (по шкале 10). С помощью головки 1 это коромысло возвращалось в исходное положение. По шкале 3 указатель 2 позволял определять угол α закручивания нити. Общий угол закручивания нити φ = γ + α. Сила же взаимодействия шариков была пропорциональна φ, то есть по углу закручивания можно судить о величине этой силы.

При неизменном расстоянии между шариками (оно фиксировалось по шкале 10 в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.

Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7 или 8) с таким же по размерам незаряженным (шарик 12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось, что сила прямо пропорциональна произведению зарядов шариков:

Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом. После сообщения шарикам заряда (он был у них одинаковый) коромысло отклонялось на некоторый угол γ. Затем поворотом головки 1 уменьшался этот угол до γ₁. Общий угол закручивания φ₁ = α₁ + (γ — γ₁)(α₁ – угол поворота головки). При уменьшении углового расстояния шариков до γ₂ общий угол закручивания φ₂ = α₂ + (γ — γ₂) . Было замечено, что, если γ₁ = 2γ₂, ТО φ₂ = 4φ₁, т. е. при уменьшении расстояния в 2 раза сила взаимодействия возрастала в 4 раза. Во столько же раз увеличился момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а значит, и сила (плечо силы оставалось неизменным). Отсюда вытекает вывод: сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними:

Дата: 29.04.2015

Литература

1. Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.

2. Вольштейн С. Л. и др. Методы физической науки в школе: Пособие для учителя / С.Л. Вольштейн, С.В. Позойский, В.В. Усанов; Под ред. С.Л. Вольштейна. – Мн.: Нар. асвета, 1988. – 144 с.

Закон Кулона. Точечный заряд.

Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.

Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.

Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:

Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:

F = k · (|q1| · |q2|) / r2

где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.

Коэффициент k в СИ принято записывать в форме:

k = 1 / (4πε0ε)

где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.

Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.

Сила взаимодействия неподвижных точечных зарядов в вакууме:

F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]

Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:

F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]

Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.

Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).

Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.

Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:

F1,2 = -F2,1

Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.

Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).

Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.

Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.

В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с

, на одном конце которой закреплён металлический шарика , а на другом противовесd . Верхний конец нити закреплён на вращающейся головке приборае , угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарикb , неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шарикамиa иb при различных их положениях.

Рис. 1.10. Опыт Кулона (крутильные весы).

При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.

Кратные и дольные единицы[ | ]

Образуются с помощью стандартных приставок СИ.

Кратные	Дольные
величина	название	обозначение	величина	название	обозначение
101 Кл	декакулон	даКл	daC	10−1 Кл	децикулон	дКл	dC
102 Кл	гектокулон	гКл	hC	10−2 Кл	сантикулон	сКл	cC
103 Кл	килокулон	кКл	kC	10−3 Кл	милликулон	мКл	mC
106 Кл	мегакулон	МКл	MC	10−6 Кл	микрокулон	мкКл	µC
109 Кл	гигакулон	ГКл	GC	10−9 Кл	нанокулон	нКл	nC
1012 Кл	теракулон	ТКл	TC	10−12 Кл	пикокулон	пКл	pC
1015 Кл	петакулон	ПКл	PC	10−15 Кл	фемтокулон	фКл	fC
1018 Кл	эксакулон	ЭКл	EC	10−18 Кл	аттокулон	аКл	aC
1021 Кл	зеттакулон	ЗКл	ZC	10−21 Кл	зептокулон	зКл	zC
1024 Кл	иоттакулон	ИКл	YC	10−24 Кл	иоктокулон	иКл	yC
рекомендовано к применению применять не рекомендуется